Rules of Thumb: Scale-up
Scale-up is hard-wired into chemical engineering, with one textbook even claiming it is the profession's raison d’etre. Jamie Cleaver looks at the principles of scale-up from an equipment-based viewpoint using the example of agitated tanks
THE CHALLENGES of scale-up are partly theoretical, partly practical, and partly conceptual. Conceptual difficulties arise because the subject means different things to different people. Some consider scale-up to involve a large amount of process development, which requires a systems engineering approach. Others have an equipment-based view of scale-up, which involves a unit operations approach. Both wviews are correct and valid. It just means that there is scope for confusion in scale-up conversations. In this article we work within the unit operations interpretation of scale-up.
It is quite common for the scale-up process to be reversed. Scale-down is particularly useful when studying the operation of large-scale plant. We can use the same principles when repurposing an existing unit operation to process a different material. This is called scale-across. Here we will use the term scale-up, knowing that the principles apply also when scaling down or scaling across.
Because scale-up is implicated throughout chemical engineering, we cannot specify a unique scale-up strategy that fits all processes. Mixing in agitated tanks works well for studying scale-up because it is perhaps the most universal process operation, used for blending, dispersing, suspending, and reacting operations. It’s also a suitable candidate for developing a checklist for process equipment scale-up. My hope is that you might be able to use the tank-mixing approach and the checklist to develop suitable strategies for your own scale-up challenges.
Start with the end in mind
The essential first principle is to make sure the equipment we are scaling up from is going to represent the larger-scale process. If our target scale is likely to be a flow reactor, let’s not try and scale up from a conical flask in a water bath. We need to build a lab-scale flow reactor. In the case of agitated tanks, we start making our design choices at the lab-scale. For example, we select an impeller design, depending on whether we need axial or radial mixing. Similarly, we make a choice on the ratio of tank diameter to impeller diameter (DT/D). Other early choices to make are the aspect ratio of liquid height to tank diameter (H/DT), and the relative size and position of baffles. Starting with the end in mind is more straightforward when scaling down or scaling across because the initial system geometry is predefined.
Understand governing mechanisms
For any process operation, successful scale-up in any direction requires knowledge of the governing mechanisms. Even in a simple operation such as liquid blending, mixing occurs through three simultaneous mechanisms:
- Distribution (macro-mixing): Mixing through bulk liquid motion from the pumping action of the impeller
- Dispersion (meso-mixing): Mixing through the rotational motion of eddies from turbulent flow
- Diffusion (micro-mixing): Mixing through molecular diffusion, driven by local differences in component concentration
These three mechanisms operate at different time- and length-scales. The significance and impact of a mechanism depends upon the application and the length scale involved. Understanding these mechanisms will assist in selecting the most appropriate impeller design for fluid blending.
Agitated tank operations involving physical or chemical changes have multiple transport mechanisms for heat transfer, mass transfer, and chemical or physical kinetics. These are superimposed on the mixing mechanisms. Reliable scale-up requires a knowledge of the contribution from each mechanism, their interaction, and the rate-limiting step.
Finally, it’s important to know the relevant physical properties of the material in terms of rheology, and stability. If the system involves bubbles of gas, solid particles, or liquid droplets in suspension there will be interplay between the distributed phase properties and the bulk rheology and mixing behaviour.
Choose the extent of scaling
How big or small is the target process operation? This is often considered in terms of the production rate or capacity. For many operations such as agitated tank processes, the production rate scales directly with the volume of the system. There is no fixed rule about the size of jump between the initial scale and the target scale. Usually the move is from lab-scale to full-scale via a pilot-scale. The pilot-scale must be sufficiently large to provide representative information for the full-scale design. In this way, we minimise the risk of poor process performance and long commissioning times.
Typically for a new agitated vessel we will operate at the litre-scale in the lab. If we are aiming for a final production scale of 10,000 L, we might aim for a pilot-scale unit of 500–1,000 L.
Geometric similarity
Ideally, we try to maintain geometric similarity between the equipment at different scales to remove extra uncertainty during scale-up. Geometric similarity means maintaining the proportions of the linear dimensions. For our agitated tank, we have the parameters defined in Figure 1.
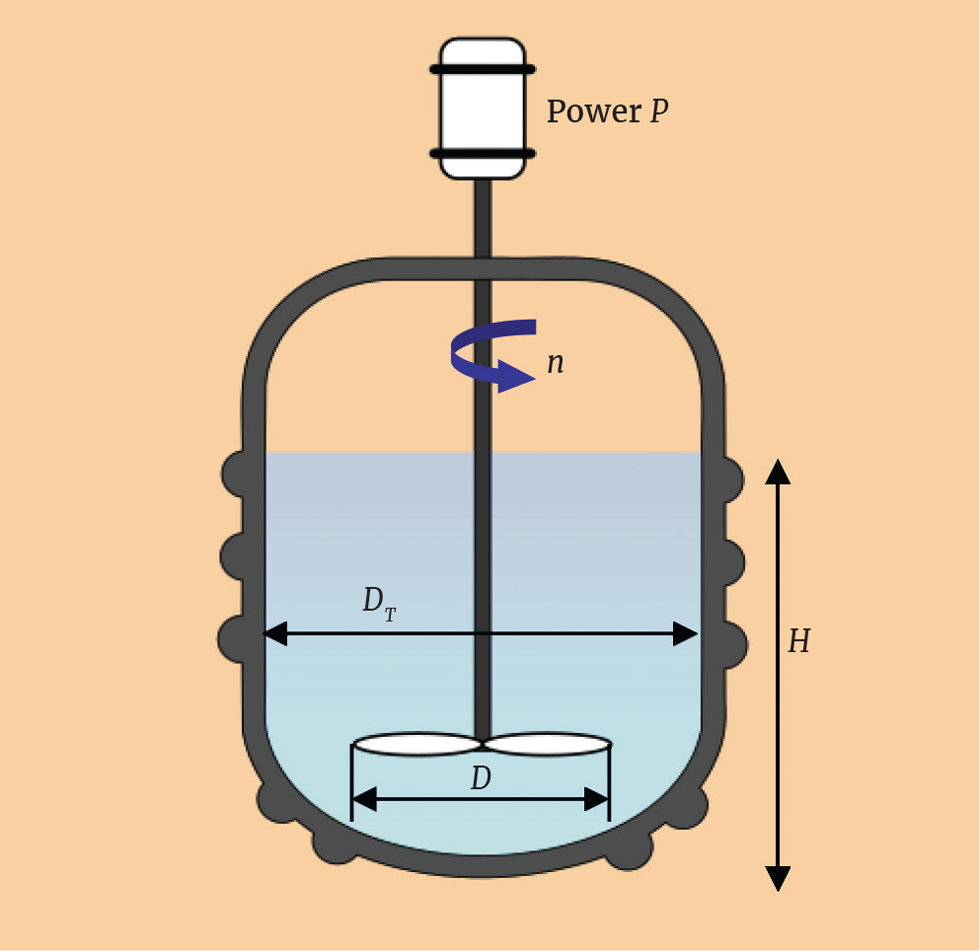
We can write the following proportionality relationships, where the subscripts 1 and 2 denote the initial scale and the target scale respectively.

Knowing the volume scale factor, we can determine the ratios of the heat transfer areas and the impeller diameters. Note that increasing the volume does not give a pro-rata increase in the heat transfer area. We see that:
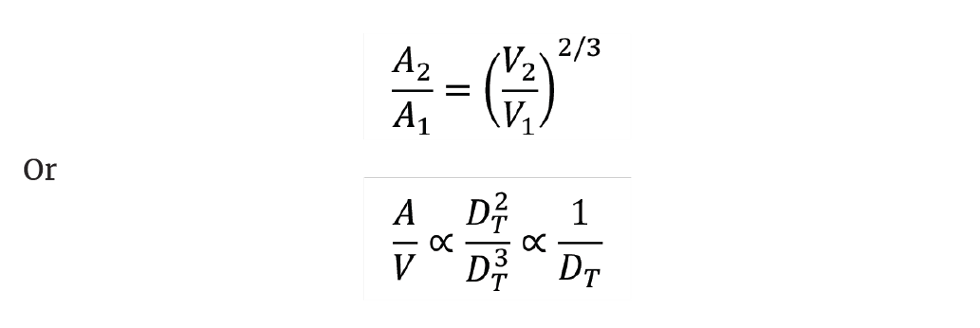
So, a volume increase of 1,000 only provides an increase in heat transfer area of 100 if we maintain geometric similarity. The heat generation rate from an exothermic reaction rises in proportion to the reactor volume. As the effective heat transfer area per unit volume decreases on scale-up there is a risk that we no longer have the capacity to remove the exotherm safely and a thermal runaway might ensue. This situation has occurred all too frequently, leading to serious process accidents.
Sometimes it is not possible to maintain geometric similarity for practical reasons or operational reasons. The loss of heat transfer area per unit volume being a case in point. In this situation it might be better to provide extra heat transfer area.
Impeller Reynolds number
Now we have established the physical size and nature of the target equipment, we have some important decisions to make about the process conditions. We must decide on the mixing intensity in the full-scale vessel, and then determine the corresponding mixing time, the impeller rotational speed and power input.
The first parameter to determine for the initial scale system is the impeller Reynolds number Rei. This is defined by:
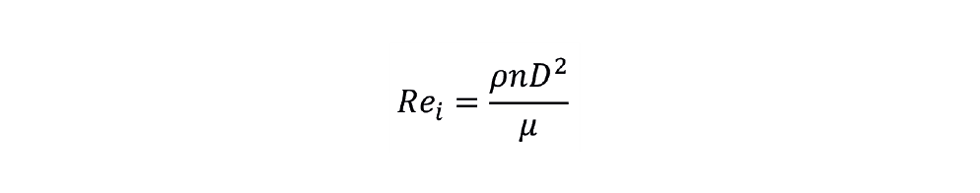
Here, ρ is the liquid density, n is the impeller rotational speed, D is the impeller diameter, and µ is the dynamic viscosity of the liquid. As usual, the Reynolds number diagnoses the transition between laminar and turbulent flow regimes, with the transition to fully turbulent mixing occurring around Rei = 104 depending on the specific impeller design.
Mixing time
The concept of mixing time (tm) is central to the successful scale-up of agitated tanks. The first step is to define how mixed is mixed. Mixing time studies normally involve introducing a shot of detectable liquid into the tank contents and monitoring the concentration with time using a probe. The extent of mixing is quantified by the magnitude of the concentration oscillations. The mixing time (t95) is defined as the time taken for the oscillations to fall within ±5% of the true value. The time for 99% mixing (t99) is defined in a similar manner.
Mixing time is clearly important for batch-blending operations. It is also critical in batch reactors. If the mixing time is long compared to the reaction half-life (t1/2), then the extent of mixing impedes the chemistry and influences the conversion. As a rule-of-thumb, mixing is not a problem if t1/2≥8tm. A similar situation arises for continuous stirred tank reactors (CSTRs). The minimum requirement is for the mean residence time (τ) to be at least 3tm. Having τ ≥ 10tm moves the CSTR towards the perfect mixing assumption.
Now let’s explore how mixing time behaves during scale-up. From another rule-of-thumb, 99% mixing (t99) occurs once the tank volume makes five passes through the impeller “pump” during turbulent conditions. The volume flow rate of liquid (q) displaced by the impeller is proportional to nD3. For a standard six-blade turbine, the following correlation predicts the value of q:
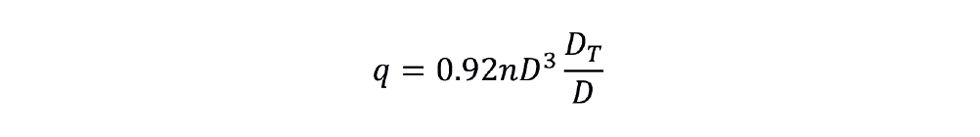
Given that it takes five passes of the tank volume through the impeller for a tank to be mixed, we can determine the mixing time as follows:
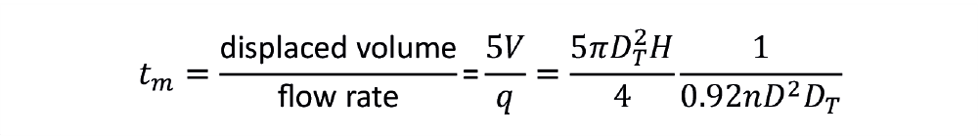
Or rearranging in dimensionless groups:
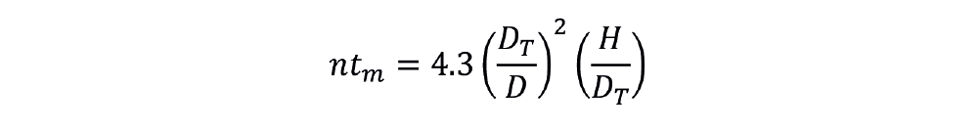
Here, ntm is the dimensionless mixing time. A value of ntm= 39 arises for a typical tank having DT = 3D, and H = DT. We can now use this information to predict the new mixing time if the value of impeller speed changes during scale-up. Remember this applies to one specific design of impeller and tank geometry during turbulent mixing. Other correlations exist for various impeller designs and tank geometries. Mixing under laminar conditions yields dimensionless mixing times in the order of 100–1,000. The prediction of laminar mixing times is more uncertain and may require some experimentation.
Impeller power input
The next step is to determine the power input to the fluid from the agitator. For a baffled tank with a single-phase liquid, all the agitator energy goes into fluid motion. Dimensional analysis reveals two dimensionless groups relating the agitator power P, the impeller rotational speed n, the impeller diameter D and the relevant liquid properties. These groups are the power number NP and the impeller Reynolds number Rei. Hence,
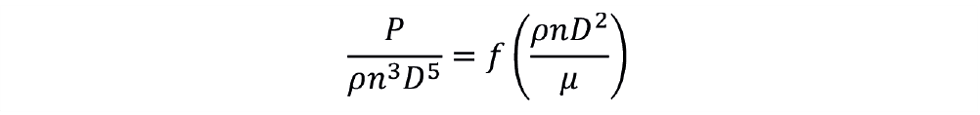
Or
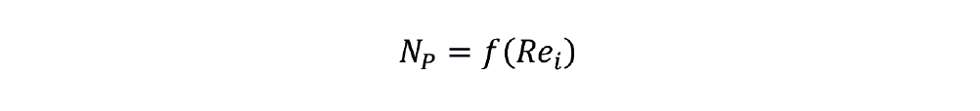
The exact nature of this relationship depends on the specific impeller design. However, there are two universal features of this relationship:
- In the turbulent mixing regime (Rei > 104), NP is constant:
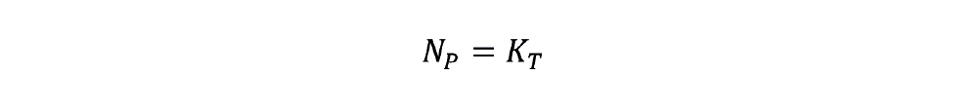
- In the laminar mixing regime, (Rei < 10), NP, is inversely proportional to Rei:
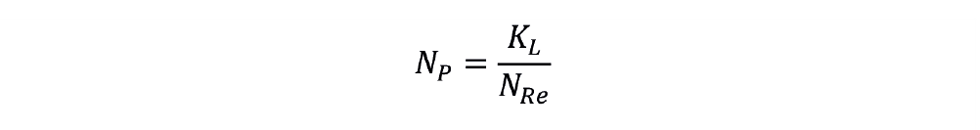
We can find values of KT and KL published for various impeller designs.
Scale-up options
Depending on our process operation, we now have some decisions to make for the scale-up of our agitated tank. Maybe we decide to maintain the same level of micro-scale turbulence, in which case it would make sense to maintain a constant ratio of agitator power input per unit volume (P/V = constant). Or maybe we have a shear-sensitive material, in which case we decide to maintain a constant impeller tip velocity, (πDn = constant). Alternatively, we might decide that a constant mixing time (tm) is important. Given that ntm is often constant during scale-up, it is clear that constant mixing time requires constant impeller rotational speed across the length scales (n = constant).
Let’s look at the procedure for assessing these three scenarios.
Constant P/V
For turbulent mixing we know that the power number NP is constant. Assuming the liquid density doesn’t change, we get:
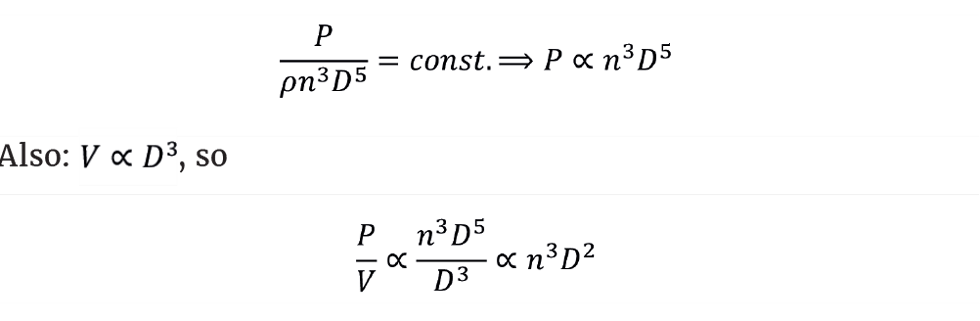
In a more useful form:
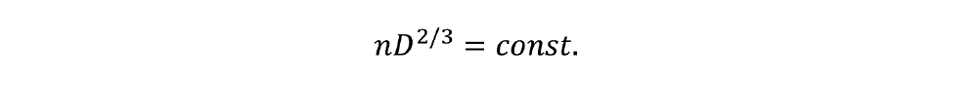
Hence, we can find the new impeller rotational speed at the target scale for the condition of constant P/V.
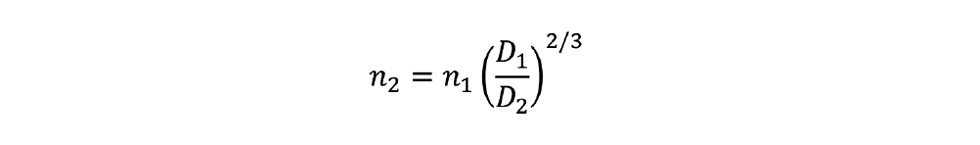
The new power requirement is given by:
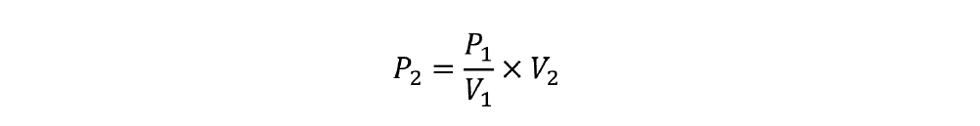
Constant impeller tip velocity, (πDn = constant)
In this situation we can relate the initial scale and target scale conditions as follows:
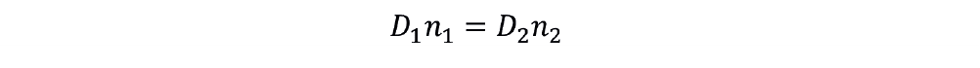
The new impeller speed is therefore:
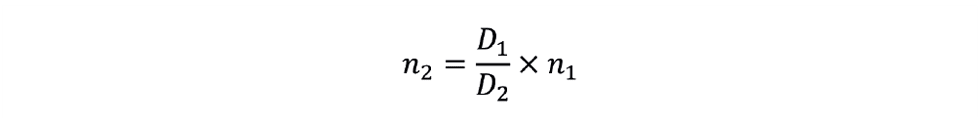
The new power requirement for constant impeller tip velocity comes from combining the conditions of constant NP and constant πDn as follows:
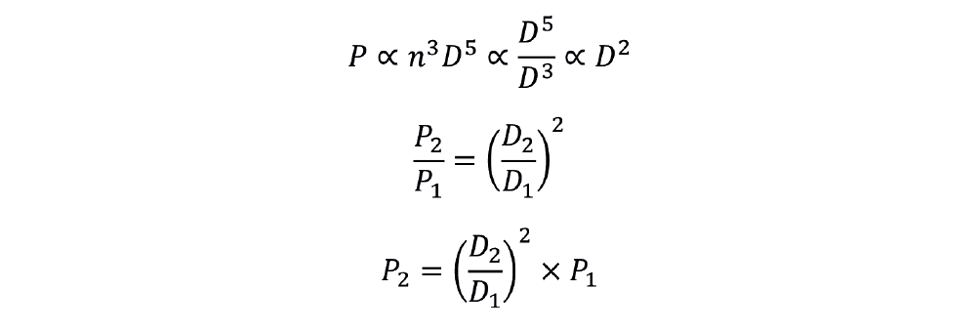
Constant impeller rotational speed, (n = constant)
We can combine the conditions of constant NP and constant n to determine power requirement for this scale-up condition as follows:
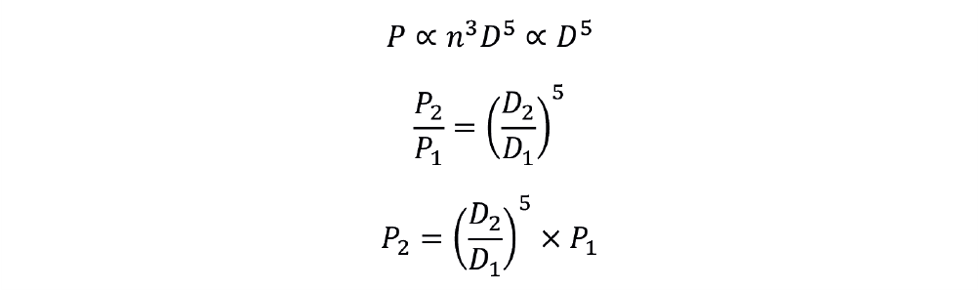
Summary of scale-up criteria
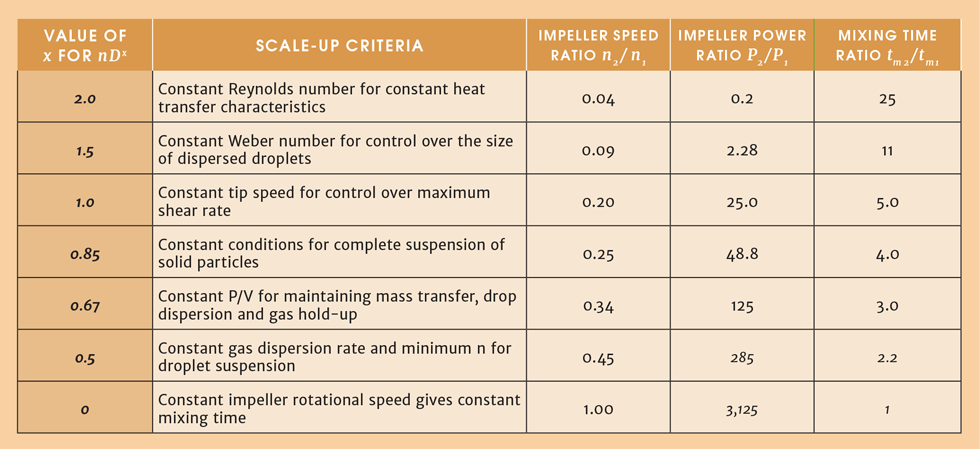
We have seen three scale-up criteria for turbulent mixing in an agitated tank, each one providing different mixing conditions for the same liquid, and each requiring a different combination of power input and impeller rotational speed. There are more criteria we could consider, depending on what is most important to maintain across the scales. We might want to maintain constant impeller Reynolds number, which corresponds to maintaining heat transfer characteristics. In other applications we might want to maintain the minimum agitator speed to keep particles in suspension, or maintain the dispersion of immiscible liquids, or provide for constant mass transfer in a gas-sparged agitated tank. The predictive correlations for these phenomena yield an expression of the form nDx = constant, where x takes on different values according to the specific scale-up criterion. The following table summarises these scenarios, and presents the impact on impeller speed and agitator power for an increase in tank liquid volume V2/V1 = 125 (D2/D1 = 5).
It’s clear from Table 1 that there is a wide range of options to choose from when scaling up an agitated tank. To make an informed choice about what to preserve over the length-scales, we need to understand the prevailing mechanisms. Note the energy penalty increases prohibitively as the ratio of impeller speeds (n2/n1) approaches unity. In practice, the most common scale-up choice is to maintain P/V constant, but this will not be suitable for all applications. The article by Thomas Post1 listed below is a good starting point to help you understand the real world of mixing.
Agitated tank complexities
In this illustration of process scale-up we have considered simple systems and explored the complexity arising from different mixing applications. Further complexity arises from the following factors:
- non-Newtonian rheology
- laminar flow
- temperature-dependent flow properties
- time-dependent flow properties
- breaking with geometric similarity
- repurposing existing equipment (scale-across)
In complex cases the same principles apply. Develop a detailed understanding of the prevailing mechanisms that control the process, and then build a scale-up strategy around those mechanisms. Most likely you will have to engage in some experimentation and maybe some process modelling. David Dickey provides a good starting point for tackling difficult mixing problems is his article Tackling Difficult Mixing Problems.2 We should note here that there are several practical problems encountered with scaling agitated tanks which add to the complexity. We will save this topic for discussion on another occasion.
Generic scale-up checklist
Now that we have been through the example of agitated tank scale-up for different process scenarios, let’s see if we can draw on this to pull together a general checklist for scale-up of a particular piece of process equipment.
1. Start with the end in mind. In other words, make sure that your initial scale system is as close as possible to the target scale in terms of geometry and mode of operation.
2. Determine your scale factor. What’s your final target scale? What would be a sensible intermediate pilot-scale? There are no rules here other than minimising risk and maximising reward.
3. Develop full mass- and energy-balances for the initial scale process and use these to develop the target-scale mass- and energy-balances.
4. Establish the governing mechanisms. Study the mechanisms that are active in your system. What are the governing physical and chemical phenomena? Most importantly, what is the rate-determining step, and how will this be influenced by a change in scale?
5. What material complexities might you face, for
example temperature-dependence, complex rheology, stability etc?
6. Develop target-scale equipment dimensions and process variables using ratios based on established correlations.
7. Determine the effect of scale-up on the capacity for heat transfer and mass transfer as the A/V ratio will decrease with increasing scale.
8. Anticipate the practical challenges. Anything involving powders is likely to behave unpredictably. Other problems occur at scale, such as foaming, deposition, accumulation of inerts, or impurities.
9. Consider down-tuning your small-scale equipment so that it represents the conditions in your larger-scale system.
10. Conduct a safety review of the concept to identify potential hazards and associated risks.
Now we have a checklist for scaling a piece of process equipment, the next stage would be to develop the full process by good design practice.
References
1. Thomas Post, Understand the Real World of Mixing, www.aiche/cep March 2010 https://postmixing.com/publications/100315ceparticle.pdf
2. David S Dickey, Tackling Difficult Mixing Problems, www.aiche/cep August 2015 https://www.aiche.org/sites/default/files/cep/20150835.pdf
3. McCabe, Smith and Harriot, Unit Operations of Chemical Engineering, 5th edition, McGraw-Hill, 1993
This is the twenty-second in a series that provides practical insights into on-the-job problems. To read more, visit the series hub at https://www.thechemicalengineer.com/tags/rules-of-thumb
Disclaimer: This article is provided for guidance alone. Expert engineering advice should be sought before application.
Recent Editions
Catch up on the latest news, views and jobs from The Chemical Engineer. Below are the four latest issues. View a wider selection of the archive from within the Magazine section of this site.




