Rules of Thumb: Pressure Drop Due to Friction

Stephen Hall offers practical tips on calculating pressure loss due to friction

THE Darcy-Weisbach equation is widely used to calculate pressure loss due to friction for liquids in pipelines. It is also sufficiently accurate for gases for most applications if the pressure drop is less than about 10% of the inlet pressure; the expansion of the gas as it loses pressure isn’t enough to throw the calculation out of its range of accuracy.

The equation depends on the Darcy (or Moody) friction factor, an empirically-derived value that was read from a chart that was originally published in 1944. This necessitates a multi-step procedure to apply Darcy-Weisbach:

• calculate the Reynolds number;
• look up the friction factor (or calculate it from one of the many formulations that replicate the chart); and
• calculate the pressure loss.

The beauty of Darcy-Weisbach is that it applies to any Newtonian fluid, pipes with smooth or rough internal surfaces, and any flow rate. By restricting its use to water or natural gas, the equation can be simplified by incorporating the density and viscosity of the specified fluid into a parameter in the simplified equation. For example the Hazen-Williams equation is used to design water pipelines; the Weymouth and Panhandle equations are for natural gas.

Here is a handy simplified formula that is applicable to any Newtonian fluid, but is restricted to turbulent flow (Reynolds number >4,000) and commercial steel pipes (roughness = 0.045 mm). For smooth tubes such as glass or polished stainless steel, use coefficient 0.014 instead of 0.016.

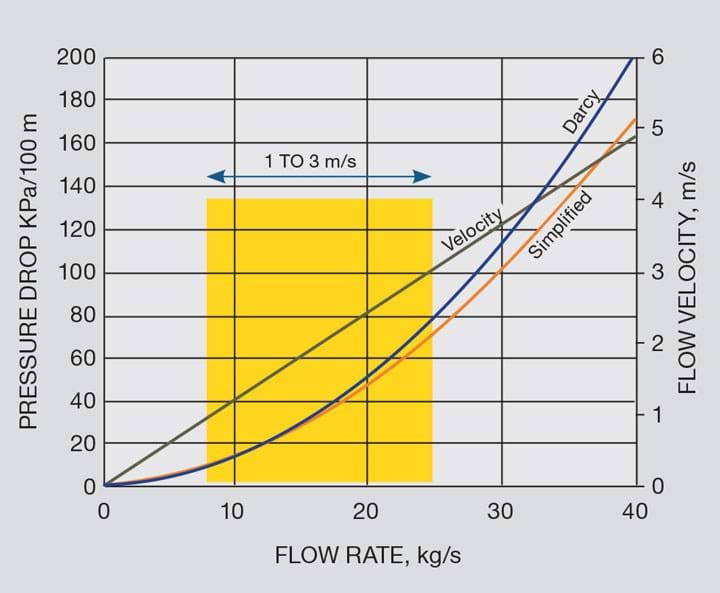
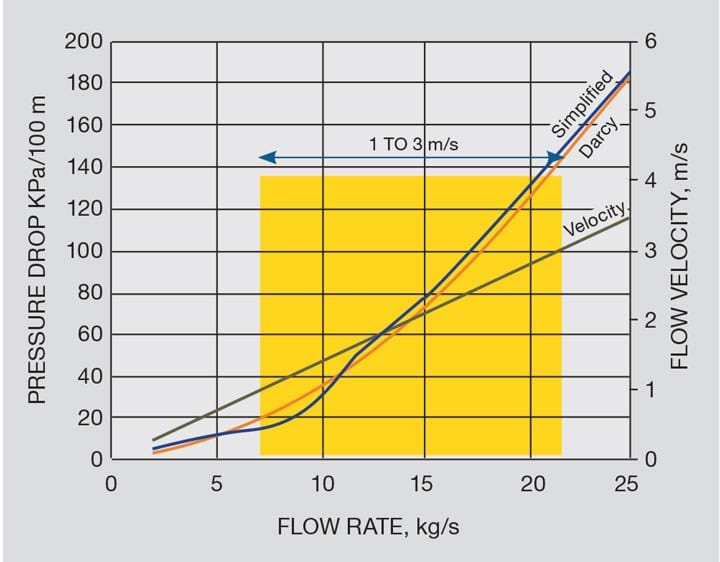
Before embracing a simplified approach, test it by comparing its results to a validated standard. The results for the simplified formula are within 10% of the Darcy-Weisbach equation in the range of 0.3–3 m/s flow velocity (Reynolds number 2,700–340,000). Repeating the comparison with Therminol at a viscosity of 0.050 Pa-s again gives excellent agreement in the turbulent range from Reynolds number above 3,000. But the velocity must exceed 1.5 m/s to be in that range. As seen in the third chart the simplified formula is applicable over a range of Reynolds numbers, not specific pressure drop or velocity.