Modelling Communication

What proportion of the original information typically gets retained by people on the receiving end of your presentation, or your report?

WELCOME to this regular slot that focuses on professional skills for chemical engineers. This month we return to our original theme of communication, by aiming to extract value from one of the most established mathematical models in engineering. Yes really! 

I frequently ask people the following question:  What proportion of the original information typically gets retained by people on the receiving end of your presentation, or your report? I have had answers ranging from 5% to 60%. Of course, there is no single answer to this question; the retention factor depends upon the material, how it is delivered, and the competence (or patience) of the listener or reader. Most people agree that low retention is a bad thing, but many seem resigned to accept that this is the way of the world. This concerns me. My next question is: whatever the retention factor, what could you do to increase it? We can answer this by turning to the Shannon and Weaver model.

Shannon and Weaver model

Claude Shannon was a mathematician who worked at the Bell Laboratories in the US. He originally published A Mathematical Theory of Communication in 1948 to help improve telecommunications. Realising that the theory had wider potential, Warren Weaver and Shannon co-authored The Mathematical Theory of Communication which was published in 1949¹. This model has been cited as “the mother of all models” and forms the basis of what is commonly known as information theory. It also forms the basis of social communication models used by psychologists, and although its application has been contentious in this context, it is of great help.

The model describes the passage of information or “facts” from a sender to a receiver and is summarised by the following diagram:

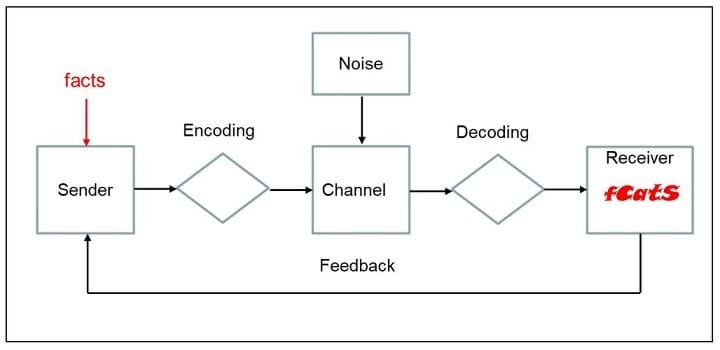
Let’s examine the main aspects of the model.

Encoding

The sender wishes to convey some facts, eg data, some logical argument, or other piece of information. The sender encodes the information by summarising it, ordering it, emphasising certain bits, or omitting other bits that might be irrelevant. This might optimise the message, but also might incur some loss or distortion of the original information. As authors or presenters, we need to make sure that we minimise these encoding losses.  This can be tricky, as we might subconsciously go into more detail about aspects of the information we like, and say less about the aspects we dislike, disagree with, or don’t understand.

Channel

This is straightforward. It is the means by which the message is transmitted. For the written word, the channel would be the physical document or the device displaying it. For a presentation, the channel would be the room, including any audio-visual facilities.

Noise

This represents any distraction that is competing for the information on the channel. For a piece of writing, the noise may be poor formatting, grammatical, or proof-reading errors, or poor printing. For a presentation, noise might be background noise or poor audio-visual reproduction. As message “senders” we should do all in our power to minimise the noise and maximise the signal-to-noise ratio.

Decoding

Decoding is the process by which a reader, or an audience member makes sense of the information they receive. Much may depend on their prior knowledge, their emotional state, and how long they have been concentrating. Other factors include any preferences or biases they may have regarding the subject. For example, if they are uncomfortable with a certain theoretical approach, or measurement technique, they might tune out of that part of the information because it does not align with their views. Decoding losses in communication are very common. How many times have you read words without taking them in, or listened to words without understanding the meaning?

Feedback

The original Shannon and Weaver model did not contain a feedback loop. It has been added later because confirmation of message receipt is an important step in the overall communication process. We receive feedback during a presentation by the extent of eye contact from the audience, and afterwards in terms of questions and comments. Similarly, we might receive feedback on a piece of written communication by the comments we get, or from the impact of our work.

What can we do?

Let’s return to the question about how to increase the retention factor of our presentations or written work. The Shannon and Weaver model usefully breaks the communication process up into steps. Like good engineers, we can evaluate the steps to diagnose where most loss is likely to occur. We can also use the model predictively. We might, for example, predict that our audience will have an aversion to an aspect of our message, such as the environmental impact. We can then compensate for this decoding loss by carefully encoding the information in such a way that values and addresses their concerns. How we might do this is another blog story for another day.

I hope that whatever the retention factor of your communication, you can use the Shannon and Weaver model to increase it.  Until next month.

Reference

1. Claude E. Shannon and Warren Weaver, 1963, The Mathematical Theory of Communication. University of Illinois Press.